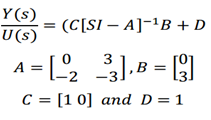Control System-1 Past Year University Question of Unit-2

Vision Institute of Technology, Kanpur

      Unit-2

2013-14

1. What is state transition matrix write its properties. Derive its expression in time & Laplace domain.
2. A multivariable system is described by the following differential equation
3. Define state variable & explain its importance & use in mathematical modelling of system.

2015-16

1. Explain controllability of the system.
2. Explain eigen vector.
3. What are advantages of state space techniques? For the given transfer function obtain the dynamic equations.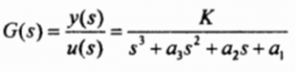4. For the following state equation , determine the transfer function.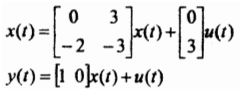
   
   

2016-17

1. Define state , State Variable, state Space & State Vector.
2. Construct the state model for a system characterized by differential equation
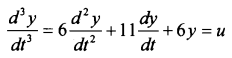   give block diagram and signal flow graph representation of state model.

3. Obtain the time response of the following system.
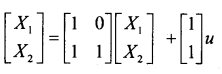   where U(t) is the unit step occurring at t=o and X^T(0)=[1 0]

2017-18

1. Write the condition of a system to be controllable.
2. A linear time invariant system is characterized by the state variable model. Examine the controllability and observability of the system.
   
   
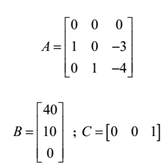
3. A system is described by the following differential equation . Represent the system in the state space.
   
   

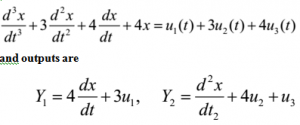
2018-19

1. For the following state equation, determine the transfer function Y(s)/U(s) Where u(t) is a unit step occurring at t=0 and XT(0)=[1 0]

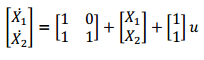
2. What is state transition matrix? Write its properties. Derive its expression in time and Laplace domains.
3. For the following state equation, determine the transfer function between Y(s)U(s) according to the formula: